Содержание:

Определение числа пи

Определение

Число $\pi$ (пи) - это константа, которая выражает отношение длины окружности к диаметру.

Число $\pi$ является иррациональным числом, то есть не может быть выражено рациональной дробью$\frac{m}{n}$ , а является бесконечной непериодической десятичной дробью $3,1414926535$ . В обиходе вполне достаточно знать три цифры числа $\pi-3,14$ ; но для более точных расчетов этого не достаточно. Для упрощения запоминания числа $\pi$ было придумано двустишие по правилам старой русской орфографии, которое позволяло легко запомнить одиннадцать его знаков:

Кто и шутя, и скоро пожелаетъ
"Пи" узнать число - ужъ знаетъ.

Для определения числа $\pi$ по нему, необходимо, сосчитать количество букв в каждом слове и написать эти цифры подряд (первую цифру отделить запятой).

В обычных условиях приближенное значение $\pi$ можно получить следующим образом:

  1. Взять круг, обмотать по краю круга нитью один раз.
  2. Измерить длину нити.
  3. Измерить диаметр круга.
  4. Разделить длину нити на длину диаметра. Получили число $\pi$ .

Например. Возьмем круг с диаметром $d=3$ см, замеряем ниткой длину окружности, получаем $l=9,3$ см. Находим отношения длины окружности к диаметру, тогда $\pi \approx \frac{9,3}{3}=3,1$ .

В каких формулах используется число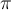

Площадь круга радиуса $r : S=\pi r^{2}$

Длина окружности радиуса $r : l=2 \pi r$

Площадь сектора с угловой величиной дуги $\alpha^{\circ} : S_{\operatorname{сект}}=\frac{\pi r^{2} \alpha}{360}$

Объем цилиндра: $V=\pi R^{2} H$

Площадь боковой и полной поверхности цилиндра:

$S_{бок}=2 \pi R H$   и  $S_{цил}=2 \pi R H+2 \pi R^{2}$

Объем конуса: $V_{кон}=\frac{\pi R^{2} H}{3}$

Площадь боковой поверхности конуса: $S_{бок}=\pi R L$

Площадь сферы: $S=4 \pi R^{2}$

Объем шара: $V=\frac{4}{3} \pi R^{3}$

Пример

Задание. Вычислить объем и полную площадь поверхности цилиндра, если радиус основания цилиндра $R=2$ см, а высота цилиндра $H=5$ см .

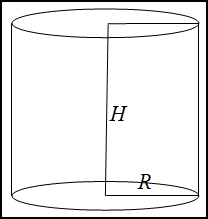
Решение. Объем цилиндра найдем по формуле

$$V=\pi R^{2} H$$

полагая $\pi=3,14$ и подставляя заданные значения, получим

$V=3,14 \cdot 2^{2} \cdot 5=3,14 \cdot 4 \cdot 5=62,8$ (см3)

Для нахождения полной площади поверхности цилиндра воспользуемся формулой

$$S_{цил}=2 \pi R H+2 \pi R^{2}$$

подставляя заданные значения, имеем

$S_{цил}=2 \cdot 3,14 \cdot 2 \cdot 5+2 \cdot 3,14 \cdot 2^{2}=87,59$ (см2)

Ответ. $V=62,8$ (см3)

            $S_{цил}=87,59$ (см2)

Все формулы объема Расчет объема цилиндра онлайн

Читать дальше: что такое действительное число.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 460 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!