Содержание:
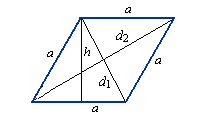
Ромб - это четырёхугольник, у которого все стороны равны. Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.
Формулы площади ромба:
Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади ромба выражается числом заключающихся в него квадратных единиц.
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
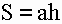
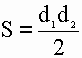
S - площадь ромба
a - длина основания ромба
h - длина высоты ромба
d1 - длина 1-ой диагонали
d2 - длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула периметра ромба:
Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
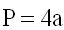
P - периметр ромба
a - длина стороны ромба
Остались вопросы?
Здесь вы найдете ответы.
Высота ромба представляет собой перпендикуляр, который опущен из одного из его углов на сторону, противоположную данному углу.
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после чего получим треугольник АВН с прямым углом. Известно, что длина всех сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и используя теорему, которая является обратной теореме о 30-градусном угле, можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно найти неизвестную величину третьего угла треугольника:
BAH=180-30-90=60 градусов.
Так, угол АВС равен:
ABC=180-60=120 градусов.
Известна формула площади (S) ромба, которая представляет собой произведение длины его стороны (а) на высоту (h), проведенную к ней:
S = a*h.
Есть возможность выразить высоту из приведенной выше формулы. Она будет равна отношению площади ромба к длине его стороны:
h = S/a.
Площадь (S) треугольника с прямым углом рассчитывается путем деления пополам произведения длин его катетов. В данном случае она будет равна:
SΔ = 4*3/2 = 6 см.кв.
Площадь ромба определяется умножением длины его стороны на высоту, проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба равна площади прямоугольного треугольника (6 см.кв.), то:
S = 5*x = 6 см.кв.
Отсюда можно найти значение х:
х = 6/5 = 1,2 см.
Ответ: высота ромба составляет 1,2 см.
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника, которые являются равными. Длины катетов этих треугольников составляют 3 см. и 4 см. Такой вывод можно сделать на основании того, что в точке пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников представляет собой сторону ромба. Ее длина равна:
с = √(9+16) = √25 = 5 см.
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба, в которой длина его стороны (а) умножается на высоту(h):
S = a*h
Из данной формулы выражаем высоту:
h = S/a = 24/5 = 4,8 см.
Ответ: Высота ромба составляет 4,8 см.
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) – известные величинами. В этом случае для определения неизвестной высоты следует пользоваться приведенной ниже формулой:
h = (d1 * d2)/a
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по следующей формуле:
Р = а+а+а+а
В данном случае периметр ромба равен 48 см., это значит, что:
а+а+а+а = 48 см.
Находим значение а:
а = 48/4 = 12 см.
Площадь ромба (S) является произведением длины его стороны (а) и высоты (h), проведенной к этой стороне:
S = а*h
В задании сказано, что площадь ромба – 60 см.кв. Значит:
а*h=60
Находим неизвестную высоту:
h=60/а=60/12=5 см.
Ответ: Высота ромба – 5 см.
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую длину. Из этого следует, что длина одной стороны будет равна ¼ части его периметра:
а = Р/4 = 32/4 = 8 см.
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на высоту (h), проведенную к ней:
S = а* h
В конкретном случае:
48 = 8* h
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
H = 48/8 = 6 см.
Ответ: Высота ромба составляет 6 см.
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых равны. Это значит:
Р = 4*а
По условию задачи:
52 = 4*а
Следовательно:
а = 52/13 = 13 см.
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина второй его диагонали будет выглядеть как 24х. Отношение их длин можно записать в следующем виде:
10х:24х=10:24
Доказано, что диагонали ромба взаимно перпендикулярны и в точке пересечения они делятся пополам, при этом образуя четыре равных треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую степень, равна длине гипотенузы, которая также возведена в квадрат:
с2 = а2 + b2
Для данной задачи это равенство записывается так:
(5х)²+(12х)²=13²
Отсюда видно, что:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
S = d₁*d₂/2 или a·h
Из этого можно составить следующее уравнение:
d₁*d₂=2a*h
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно сделать, рассмотрев все треугольные фигуры, элементами которых являются эти высоты. Есть возожность высчитать высоту ромба при помощи различных параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В этом случае высота ромба будет равна отношению его площади к длине высоты: h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся между смежными сторонами, то для расчета высоты ромба используется следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на основании того, какие величины будут известны по условию задания. Однако ключевыми параметрами, используя которые можно вычислить высоту ромба, являются диагонали, длина любой его стороны и угол, образованный между смежными сторонами.
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a — сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Р/4 = 8 см.
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь можем определить длину высоты:
h = 8-1,7 = 6,3 см.
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее опущена:
8 * 6,3 = 50,4 см².кв.
Ответ: S = 50,4 см. кв.
Если длины диагоналей фигуры относятся как 4/3, то их половины будут относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Отсюда:
25d²=100
d =2,
Значит:
d¹/2 = 4d = 8 см.
d²/2 = 3d = 6 см.
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур, основанием которых является одна диагональ, а вторая диагональ ромба представляет собой сумму длин высот этих фигур. Диагонали ромба при пересечении образуют угол в 90 градусов. На основании этого можно найти площадь ромба следующим образом:
S = ½ d1*d2.
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а затем разделить полученное число на два:
S = ½ d1*d2.
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а вторая – 4 см. Тогда его площадь будет равна:
S=1/2*5*4=10 см. кв.
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и высоту (h). Формула записывается так:
S=a*h.
См. также: Программа для расчета периметра ромба.










