В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила совершает работу. Считают, что если скорость увеличивается, то работа является положительной, если скорость уменьшается, то работа, которую совершает сила – отрицательна. Изменение кинетической энергии материальной точки в ходе ее движения между двумя положениями равно работе, которую совершает сила:
$$A=\Delta E_{k}=\frac{m v_{2}^{2}}{2}-\frac{m v_{1}^{2}}{2}(1)$$Содержание:
- Определение и формула работы
- Элементарная работа
- Работа силы на конечном участке траектории
- Единицы измерения работы
- Примеры решения задач
Определение и формула работы
Определение
Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи величины перемещения, которое совершает рассматриваемое тело под действием силы ($\bar{F}$).
Элементарная работа
Элментарная реабота $(\delta A)$ некоторой силы $\bar{F}$ определяется как скалярное произведение:
$$\delta A=\bar{F} \cdot d \bar{r}=F \cdot d s \cdot \cos \alpha(2)$$$\bar{r}$ радиус – вектор точки, к которой приложена сила, $\bar{r}$ - элементарное перемещение точки по траектории, $\alpha$ – угол между векторами $d s=|d \bar{r}|$ и $d \bar{r}$. Если $\alpha$ является тупым углом работа меньше нуля, если угол $\alpha$ острый, то работа положительная, при $\alpha=\frac{\pi}{2} \delta A=0$
В декартовых координатах формула (2) имеет вид:
$$\delta A=F_{x} d x+F_{y} d y+F_{z} d z(3)$$где Fx,Fy,Fz – проекции вектора $\bar{F}$ на декартовы оси.
При рассмотрении работы силы, приложенной к материальной точке можно использовать формулу:
$$\delta A=\bar{F} \bar{v} d t=\bar{v} d \bar{p}(4)$$где $\bar{v}$ – скорость материальной точки, $\bar{p}$ – импульс материальной точки.
Если на тело (механическую систему) действуют несколько сил одновременно, то элементарная работа, которую совершают эти силы над системой, равна:
$$\delta A=\sum_{i=1}^{n} \delta A_{i}=\sum_{i=1}^{n} \bar{F}_{i} d \bar{r}_{i}=\sum_{i=1}^{n} \bar{F}_{i} \bar{v}_{i} d t(5)$$где проводится суммирование элементарных работ всех сил, dt – малый промежуток времени, за который совершается элементарная работа $\delta$ над системой.
Результирующая работа внутренних сил, даже если твердое тело движется, равна нулю.
Пусть твердое тело вращается около неподвижной точки - начала координат (или неподвижной оси, которая проходит через эту точку). В таком случае, элементарная работа всех внешних сил (допустим, что их число равно n), которые действуют на тело, равна:
$$\delta A=\bar{M} \bar{\omega} d t=\bar{M} d \bar{\varphi}(6)$$где $\bar{M}$ – результирующий момент сил относительно точки вращения, $d \bar{\varphi}$ – вектор элементарного поворота, $\bar{w}$ – мгновенная угловая скорость.
Работа силы на конечном участке траектории
Если сила выполняет работу по перемещению тела на конечном участке траектории его движения, то работа может быть найдена как:
$$A=\int_{0}^{s} \bar{F} \cdot d \bar{r}(7)$$В том случае, если вектор силы – величина постоянная на всем отрезке перемещения, то:
$$A=F_{\tau} \cdot s$$где $F_{\tau}=F \cos \alpha$ – проекция силы на касательную к траектории.
Единицы измерения работы
Основной единицей измерения момента работы в системе СИ является: [A]=Дж=Н•м
В СГС: [A]=эрг=дин•см
1Дж=107 эрг
Примеры решения задач
Пример
Задание. Материальная точка движется прямолинейно (рис.1) под воздействием силы, которая задана уравнением: $F=C \sqrt{s}(C=$ const $)$ . Сила направлена по движению материальной точки. Чему равна работа данной силы на отрезке пути от s=0 до s=s0?
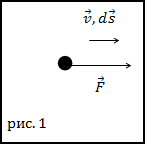
Решение. За основу решения задачи примем формулу расчёта работы вида:
$$A=\int_{0}^{s_{0}} F \cos \alpha d s(1.1)$$где $\alpha = 0$, та как по условию задачи $\bar{F} \uparrow \uparrow \bar{s}$ . Подставим выражение для модуля силы заданное условиями, возьмем интеграл:
$$A=\int_{0}^{s_{0}} F d s=\int_{0}^{s_{0}} C \sqrt{s} d s=\frac{2}{3} C s^{\frac{3}{2}}$$Ответ. $A=\frac{2}{3} C s^{\frac{3}{2}}$
Пример
Задание. Материальная точка перемещается по окружности. Ее скорость изменяется в соответствии с выражением: $v \sim t^{2}$ . При этом работа силы, которая действует на точку, пропорциональна времени: $A \sim t^{n}$ . Каково значение n?
Решение. В качестве основы для решения задачи используем формулу:
$$\delta A=\bar{F} \bar{v} d t=m\left(\bar{a}_{n}+\bar{a}_{\tau}\right) \bar{v} d t=m \bar{a}_{n} \bar{v} d t+m \bar{a}_{\tau} \bar{v} d t(2.1)$$Зная зависимость скорости от времени найдем связь тангенциальной составляющей ускорения и времени:
$$a_{\tau}=\frac{d v}{d t} \sim t(2.2)$$Нормальная составляющая ускорения будет иметь вид:
$$a_{n}=\frac{v^{2}}{R} \sim t^{4}(2.3)$$При движении по окружности нормальная составляющая ускорения будет всегда перпендикулярна вектору скорости, следовательно, вклад в произведение силы на скорость будет вносить только тангенциальная составляющая, то есть выражение (2.1) преобразуется к виду:
$$\delta A=m \bar{a}_{\tau} \bar{v} d t=m a_{\tau} v d t(2.5)$$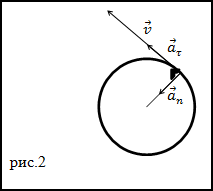
Выражение для работы найдем как:
$$A=C \int_{0}^{t} t \cdot t^{2} d t \sim t^{4}$$Ответ. n=4
Читать дальше: Формула силы Ампера.










