Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$\bar{F}, \bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
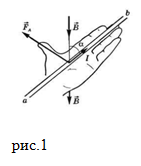
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
 большой палец укажет направление силы Ампера (рис.1).
большой палец укажет направление силы Ампера (рис.1).
Содержание:
- Определение и формула силы Ампера
- Закон Ампера
- Силы, действующие на проводники с током в магнитном поле
- Единицы измерения силы Ампера
- Примеры решения задач
Определение и формула силы Ампера
Определение
Закон Ампера
Элементарная сила Ампера ($d\bar{F}_A$) определена законом (или формулой) Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(1)$$где I – сила тока, $d \bar{l}$ – малый элемент длины проводника – это вектор, равный по модулю длине проводника, направленный в таком же направлении как вектор плотности тока, $\bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d \bar{F}_{A}=\bar{j} \times \bar{B} d V(2)$$где $\bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I \cdot B \cdot d l \cdot \sin \alpha(3)$$где $\alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$\bar{F}_{A}=I \int_{l} d \bar{l} \times \bar{B}(4)$$где $\bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl. Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I, в однородном магнитном поле действует сила Ампера равная $\bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d} d l(5)$$где d – расстояние между проводниками, $\mu_{0}=4 \pi \cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная. Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются. Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$\frac{F}{l}=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d}$$Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B \operatorname{lsin} \alpha$$где $\alpha$ – искомый угол. Следовательно:
$$\alpha=\arcsin \left(\frac{F}{I B l}\right)$$Ответ. $\alpha=\arcsin \left(\frac{F}{I B l}\right)$
Пример
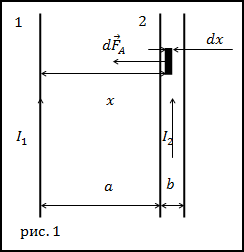
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга. Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(2.1)$$Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$где ток, который течет в элементе проводника dx, выразим как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$где из рис.1 видно, что $a \leq x \leq a+b$, по условию задачи силу следует найти на единицу длины, значит $0 \leq l \leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2.5):
$$F_{A}=\int_{a}^{a+b} \int_{0}^{1} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x d l=\int_{a}^{a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$
Читать дальше: Формула силы выталкивания.










