Задание. Найти разность чисел:
1) $17-5$ ; 2) $13-27$ ; 3) $2,34-1,24$
Ответ.
$17-5=12$
$13-27=-14$
$2,34-1,24=1,1$
Содержание:
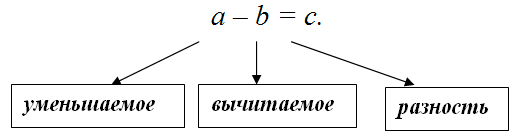
Разность $r$ чисел $a$ и $b$ - это результат вычитания числа $b$ из числа $a$ .
Пример
Задание. Найти разность чисел:
1) $17-5$ ; 2) $13-27$ ; 3) $2,34-1,24$
Ответ.
$17-5=12$
$13-27=-14$
$2,34-1,24=1,1$
В случае если вычитаются большие числа или десятичные дроби, то используют способ вычитания в столбик.
Пример
Задание. Найти разность чисел:
1) $5637-172$ ; 2) $43,56-23,94$
Решение. Найдем разность этих чисел, используя метод вычитания в столбик. В первом примере запишем числа друг под другом так, чтобы единицы были под единицами, десятки под десятками и т.д. Вычитание будем производить справа налево, вычитая из верхнего числа меньшее. В случае, если верхнее число меньше нижнего занимаем десяток у верхнего числа стоящего левее данного, при этом число стоящее левее уменьшится на единицу, а данное число увеличится на 10.
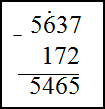
Для нахождения второй разности запишем заданные десятичные дроби в столбик так, чтобы запятая верхнего числа совпадала с запятой нижнего. После чего вычтем их в столбик как числа в первом примере.
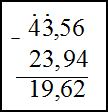
Ответ.
$5637-172=5465$
$43,56-23,94=19,62$
Разность рациональных дробей находится по правилу
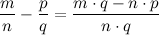
Пример
Задание. Найти разность рациональных дробей:
1) $\frac{5}{13}-\frac{2}{11}$ ; 2) $1 \frac{1}{7}-\frac{2}{5}$
Решение. По правилу вычитания рациональных дробей имеем
$$\frac{5}{13}-\frac{2}{11}=\frac{5 \cdot 11-2 \cdot 13}{13 \cdot 11}=\frac{55-26}{143}=\frac{29}{143}$$
Во втором примере, перед тем как производить вычитание дробей запишем первую дробь в виде неправильной. Для этого целую часть умножим на знаменатель и прибавим к числителю:
$$1 \frac{1}{7}-\frac{2}{5}=\frac{8}{7}-\frac{2}{5}=\frac{8 \cdot 5-2 \cdot 7}{7 \cdot 5}=\frac{40-14}{35}=\frac{26}{35}$$
Ответ.
$$\frac{5}{13}-\frac{2}{11}=\frac{29}{143}$$
$$1 \frac{1}{7}-\frac{2}{5}=\frac{26}{35}$$
Читать дальше: что такое целое число.