Условие задачи:
Дана правильная треугольная призма \( ABCA_1B_1C_1 \), стороны основания которой равны \( a \). Найдите угол между прямыми\( A_1B \) и \( AC_1 \), если сумма длин всех сторон обеих оснований равна \( AA_1 \).
Решение:
\( ABCA_1B_1C_1 \) – правильная треугольная призма => \( \Delta ABC \) и \( \Delta A_1B_1C_1 \) – правильные треугольники.
\( AB=AC=BC=A_1B_1=A_1C_1=B_1C_1=a \)
\( AA_1=BB_1=CC_1=6a \)
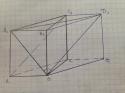
Достроим треугольную призму до правильной четырехугольной призмы (см.
рис.), в основании которой будет ромб.
Т.о. необходимо найти \( \angle A_1BD_1 \).
\( A_1B=BD_1=\sqrt{AB^2+AA_1^2}=a\sqrt{37} \)
В правильном треугольнике все углы равны между собой и равны \( \frac{\pi}{3} \). Значит в получившемся ромбе \( \angle ABD=\frac{2 \pi}{3} \).
По т.синусов:
\( \frac{AD}{\sin \large{ \frac{2 \pi}{3}}}=\frac{BD}{\sin \large{\frac{\pi}{3}}} \)
\( AD=A_1D_1=a\sqrt{3} \)
По т.косинусов:
\( A_1D_1^2=A_1B^2+BD_1^2-2A_1B\cdot BD_1\cdot \cos \angle A_1BD_1 \)
\( \angle A_1BD_1=\arccos \frac{71}{74} \)