Нужно и то и то.
Необходимо составить программу при запуске которой появлялась модель падения тела с высоты например(шар), были оси х и y, чтобы в модели можно было бы устанавливать параметры: высота(h), коэф.сопротивления(k), масса тела(m), и другое.
Также, чтобы в модели были показаны расчеты в виде таблицы, также показаны графики изменения скорости и ускорения падения тела с сопротивлением воздуха и без него.
Вводить данные - высота (h), коэф.сопротивления (k), масса(m), ...
t - индекс, показывать движение тела с учетом сопротивления воздуха и без него.
Установить в константах g=9,8 м/c^2
Примем, что тело массой m падает с высоты h с начальной скоростью Vн. Известно, что сила сопротивления среды (воздуха) пропорциональна квадрату скорости. На рисунке показана схема модели. Имеем закон Ньютона для свободно падающего тела:

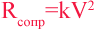
Согласно второму закону Ньютона движение под действием сил можно записать равенством
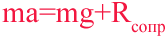
Проецируем это равенство на ось движения, подставим выражение для силы сопротивления воздуха

Получим формулу для вычисления ускорения
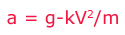
Будем рассчитывать скорость и расстояние, которое пролетел парашютист через равные промежутки времени Δt. Формула для вычисления моментов времени имеет вид:
ti+1=ti+Δt
Будем также считать, что на каждом промежутке ускорение постоянно и равно аi. Формула для вычисления ускорения имеет вид

где Vi— скорость в начале промежутка (V0 — начальная скорость).

Расстояние, которое пролетел парашютист, равно сумме расстояния, пройденного к началу очередного промежутка времени и расстояния, пройденного на этом промежутке
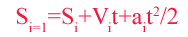
Обозначим за S перемещение тела, V - скорость, а - ускорение. Тогда в моменты времени:
to=0: So=h, Vo=Vн, ao=g; здесь So=S(to), Vo=V(to), ao=a(to);
t1=dt: S1=So+Vodt+aodt2/2, V1=Vo+aodt, a1=(mg-kV1)/m;
...
ti+1=(i+1)*dt: Si+1=Si+Vidt+aodt2/2, Vi+1=Vi+aidt, ai+1=(mg-kVi)/m;
и т.д.
Итак, имеем рекурентную формулу определения перемещения Si, скорости Vi и ускорения аi в дискретные моменты времени ti=i*dt, где i=0, 1, 2 ...